Die ›sinfonische Welle‹ als Methode der musikalischen Analyse
Richard Wagner nannte die Symmetrie vieler Musikstücke der zweiten Hälfte des 18. Jahrhunderts einmal abfällig Quadratur einer konventionellen Tonsatzkonstruktion. Versuche, die Musik Wagners und Bruckners mit neuen Modellen zu beschreiben, gehen in erster Linie auf August Halm (1869–1929) und Ernst Kurth (1886–1946) zurück. Die mit dem deutschen Musikpädagogen und österreichischen Musikwissenschaftler verbundene musikanalytische Richtung wird auch als musikalische Energetik oder musikalischer Energetismus bezeichnet. Damit ist gemeint, dass musikalische Form sich nicht mehr architektonisch, also in klar abgegrenzten Formteilen vermittelt, sondern nur im Auf- und Abbau von Spannung erlebt werden kann. In diesem Zusammenhang findet sich auch oft der Begriff Formung statt Form sowie die Metapher einer Welle: Denn eine idealtypische Welle bäumt sich auf (Spannungsaufbau), hat eine Krone (Spannungshöhepunkt) und verläuft sich wieder (Spannungsabbau). Die folgende Abbildung zeigt einen Wellenverlauf mit mehreren Wellenbergen:

Die folgende Abbildung zeigt, dass dieser Wellenverlauf den ersten Satz der 1. Sinfonie in c-Moll Op. 11 von Felix Mendelssohn recht gut beschreibt:

Hören Sie sich den ersten Satz der Sinfonie in c-Moll Op. 11 von Felix Mendelssohn an und verfolgen Sie dem musikalischen Verlauf, indem Sie insbesondere auf den Lautstärkeverlauf achten:
Warum sich die energetische Beschreibung von Musik als Methode der musikalischen Analyse nicht durchsetzen konnte, ist schwer zu sagen. Ein Grund könnte darin liegen, dass von den bekannten Persönlichkeiten, die in der ersten Hälfte des 20. Jahrhunderts gelebt und über musiktheoretische Themen geschrieben haben (wie beispielsweise der Begründer der graphischen Analyse Heinrich Schenker, der Komponist, Theoretiker und Verfechter der motivisch-thematischen Analyse Arnold Schönberg, der Begründer der Funktionsanalyse Hugo Riemann sowie Ernst Kurth als Anhänger einer energetischen Musiktheorie), nur einer keine Verbindung zum Judentum hatte: Hugo Riemann. Während seine Funktionstheorie durch Musiktheoretiker mit brauner Vergangenheit wie Paul Schenk, Hermann Grabner und Wilhelm Maler durch den Krieg hindurch rezipiert worden ist, wurde die Rezeption insbesondere der graphischen Analyse nach Schenker und der energetischen Musiktheorie nach Kurth in Deutschland durch die Nationalsozialisten unterbrochen.
Doch seit einigen Jahrzehnten gibt es eine Renaissance der in Deutschland verdrängten musikanalytischen Ansätze. Wolfgang Krebs hat sich dabei insbesondere um eine Weiterentwicklung des Instrumentariums einer energetischen Analyse von Musik bemüht. Denn an der eingangs abgebildeten Welle könnte als unbefriedigend empfunden werden, dass sie zwar die Abfolge von lauten (spannungsreichen) und leisen (entspannteren) Teilen gut beschreibt, aber an den Kanten recht ungenau ist. Ihrem relativ kontinuierlichen Auf und Ab lässt sich beispielsweise nicht entnehmen, ob ein Ereignis plötzlich eintritt oder endet. Im folgenden werden daher vier Wellenformen unterschieden und für die ersten drei davon die von Wolfgang Krebs vorgeschlagene Terminologie übernommen.
Wellenformen
Die Fluktuationswelle
Das Kurvenbild einer Fluktuationswelle ist durch einen langsamen und fließenden Anstieg, einen Höhepunkt und eine wiederum langsame Rückentwicklung charakterisiert. Die Fluktuationswelle ist eine symmetrische Erscheinung mit einer Ausdehnung von 10, 20 oder mehr Takten. Ein solcher Spannungsverlauf findet sich beispielsweise im Kopfsatz der 6. Sinfonie Op. 68 (Pastorale) von Ludwig v. Beethoven.
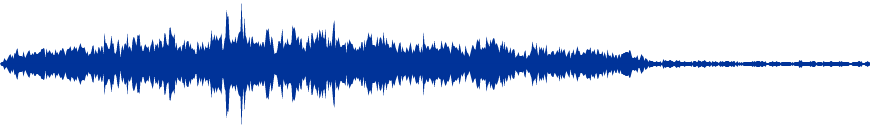
Copyright Info: Ludwig v. Beethoven, Sinfonie Nr. 6, 1. Satz, Ausschnitt, DuPage Symphony Orchestra, Ltg.: Barbara Schubert, Lizenz: CC By-NC-SA 3.0, Download: IMSLP
Die Expansionswelle
Demgegenüber weist die Expansionswelle einen langsamen und kontinuierlichen Anstieg bis zu einem Höhepunkt auf. Der Wellenkrone folgt eine relativ schnelle Rückentwicklung. Die Expansionswelle ist daher asymmetrisch, ein schönes Beispiel für diesen Spannungsverlauf findet sich zum Beginn der 2. Sinfonie (Auferstehung) von Gustav Mahler:

Copyright Info: Gustav Mahler, Sinfonie Nr. 2, 1. Satz, Anfang, DuPage Symphony Orchestra, Ltg.: Barbara Schubert, Lizenz: CC By-SA 3.0, Download: IMSLP
Die Degressionswelle
Die Degressionswelle ist durch ein plötzliches Aufbäumen bzw. eine unvermitteltes Erscheinen (z.B. durch ein plötzlich einsetzendes Orchestertutti) charakterisiert. Auch sie ist asymmetrisch, jedoch mit einem Höhepunkt am Anfang, während ihr weiterer Verlauf eine ausführliche und relativ langsame Rückentwicklung zeigt. Degressionswellen sind in der Musik des ausgehenden 19. Jahrhunderts ausgesprochen häufig anzutreffen, ein solcher Spannungsverlauf findet sich beispielsweise in der 6. Sinfonie Op. 74 von Peter I. Tschaikowsky:

Copyright Info: Peter I. Tschaikowsky, Sinfonie Nr. 6, 1. Satz, Ausschnitt, University of Chicago Orchestra, Ltg.: Barbara Schubert, Lizenz: CC By-NC-ND 3.0, Download: IMSLP
Die Blockwelle
Im Zusammenhang mit Instrumentalmusik des frühen 18. Jahrhunderts wird häufig von Terrassendynamik gesprochen. Dieser Begriff bezieht sich auf die Dynamik (also einen guten Indikator für eine hohe Spannung) und besagt, dass Lautstärkeverläufe nicht fluktuierend, sondern nach dem Modell einer Terrasse beschreibbar sind. Das Plateau der Terrasse entspricht dabei dem Parameter laut, die Umgebung dem Parameter leise. Wie die Fluktuationswelle sind Blockwellen symmetrische Erscheinungen, die einen plötzlichen Spannungsanstieg (wie die Degressionswelle) haben, aber darüber hinaus auch einen schnellen Spannungsabbau (wie die Expansionswelle). Das folgende Beispiel zeigt einen Blockwellenverlauf in der Sinfonie Hob. I:100 (Militär) von Joseph Haydn:

Copyright Info: Joseph Haydn, Sinfonie 100 (Militär), 1. Satz, Ausschnitt, Wiener Symphoniker, Ltg.: Hermann Scherchen, Lizenz: CC By-NC-SA 2.5, Download: LiberLiber
Ausblick
Die hier vorgestellten Wellenformen bilden ein gutes Instrumentarium zur Erschließung der Form höchst komplexer Orchestermusik (beispielsweise um 1900). Die Aufgabe einer wissenschaftlichen Beschäftigung mit Musik könnte es darüber hinaus sein, Modelle der Aufeinanderfolge von Wellen zu konstruieren, um so Zeit- und Personalstile theoretisch zu erschließen und deren Wirkung besser verstehen zu können. Und nicht zuletzt bieten die gezeigten Wellenformen ein methodisches Werkzeug, um im Musikunterricht allgemeinbildender Schulen Orchestermusik zu thematisieren, deren Länge einer rein auditiven Beschäftigung und deren Komplexität einer Notenanalyse entgegensteht. Nicht zuletzt lassen Spannungsverläufe eine Harmonisierung von emotionalem Erleben und theoretischem Beschreiben zu, was sich durch kein anderes musiktheoretisches Werkzeug in vergleichbarem Maße bewerkstelligen lässt. Die Konzentration auf den Spannungsverlauf einer musikalischen Passage ist zudem hilfreich, größere musikalische Abschnitte als Einheiten aufzufassen, wie das abschließende Beispiel aus dem Vorspiel zum 1. Akt der Oper Tristan und Isolde von Richard Wagner zeigt:
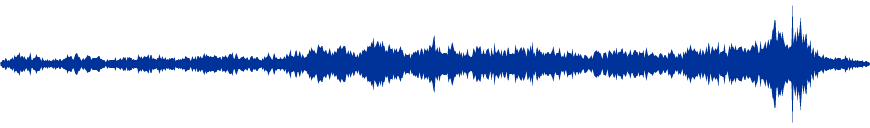
Copyright Info: Richard Wagner, Vorspiel zum 1. Akt der Oper Tristan und Isolde, Ausschnitt, Fulda Symphonic Orchestra, Ltg.: Simon Schindler, Lizenz: CC By-SA 3.0, Download: IMSLP
Literatur
- Helga de la Motte-Haber, »Kräfte im musikalischen Raum. Musikalische Energetik und das Werk von Ernst Kurth«, in: Musiktheorie (= Handbuch der Systematischen Musikwissenschaft 2), hrsg. von Helga de la Motte-Haber und Oliver Schwab-Felisch, Laaber 2005, S. 283–310.
- Wolfgang Krebs, »Zum Verhältnis musikalischer Syntax und Höhepunktgestaltung in der zweiten Hälfte des 19. Jahrhunderts«, in: Musiktheorie 13 (1998), S. 31−41.
- Wolfgang Krebs, Innere Dynamik und Energetik in Ernst Kurths Musiktheorie. Voraussetzungen, Grundzüge, analytische Perspektiven (Frankfurter Beiträge zur Musikwissenschaft 28), Tutzing 1998.
- Ernst Kurth, Bruckner, 2 Bde., Faks.-Nachdr. der Ausgabe Berlin 1925, Hildesheim 1971, 22000.
- Ulrich Kaiser. »Die Fünfte mal anders«, in: Musik und Unterricht 4/2013, S. 14-22.
- Ludwig Holtmeier, »Von der Musiktheorie zum Tonsatz. Zur Geschichte eines geschichtslosen Faches«, in: Zeitschrift der Gesellschaft für Musiktheorie 1/1 (2003), S. 11−34.
Erstellung des Beitrags: 10. September 2014
Letzte Änderung des Beitrags am 1. Oktober 2014