Eine Einführung in die Musical set theory.
Musical set theory (engl. set theory = Mengenlehre) bezeichnet den Versuch, die mathematische Mengenlehre bzw. auch die Informatik für die musikalische Analyse nutzbar zu machen. Herausragende Vertreter dieses Ansatzes sind unter anderen Allen Forte[1] und John Rahn[2] mit dem System der pitch class sets (engl. pitch = Tonhöhe, Stimmung, engl. class = Klasse, Kategorie, engl. set = Menge, Sammlung). Sie bietet ein universelles Werkzeug, Zusammenklänge, oder auch eine sukzessive Reihe von Tonhöhen zu einer Menge zusammenzufassen und diese eindeutig zu benennen. Wenngleich diese Benennung auch sehr technisch und abstrakt anmutet, so hat sie doch den Vorteil der Universalität: Sie lässt sich auch auf Musik anwenden, die sich der konventionellen, auf tonale Musik hin ausgelegten Harmonielehre entzieht, wie z. B. Zwölftonkompositionen.
pitch class (p.c.)
Eine pitch class ist die abstrakte Zusammenfassung aller Töne mit einem bestimmten „Tonhöhencharakter“, wie z. B. alle Töne, denen wir den Namen „c“ geben würden. Dabei spielt die Notation keine funktionale Rolle, d. h. auch jedes „his“ und jedes „deses“ fallen in diese Kategorie. Die Theorie geht also davon aus, dass Oktavversetzungen und enharmonische Umnotierungen eines Tones äquivalent sind. Demnach repräsentiert eine pitch class unendlich viele Töne. Folgende Töne sind zum Beispiel nur einige der Instanzen (=Repräsentanten) einer einzigen pitch class:
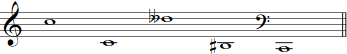
pitch interval (ip) und interval class (i. c.)
Der Abstand zweier pitches, das pitch interval wird der Einfachheit halber in Halbtönen gemessen. So beträgt der Abstand zwischen c und e 4 Halbtonschritte und kann demnach als ip4 angegeben werden. Auch Intervalle lassen sich in Klassen einteilen, wobei hier jeweils Komplementärintervalle samt ihrer Oktavversetzungen zusammengefasst werden, d. h.: Kleine Septime und große Sekunde (aber auch große None) sind Mitglieder derselben interval class. Diese interval classes werden einfach durchnummeriert, und es gibt ihrer logischerweise genau sechs verschiedene:
| i. c. | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| enthält: | kleine Sekunde, große Septime, kleine None, usw. | große Sekunde, kleine Septime, große None, usw. | kleine Terz, große Sexte, verminderte Septime, usw. | große Terz, kleine Sexte, verminderte Quarte, usw. | reine Quarte, reine Quinte, reine Undezime, usw. | Tritonus, verminderte Quinte, übermäßige Undezime, usw. |
pitch class set (p. c. set)
Als pitch class set bezeichnet man die konkrete Zusammenfassung verschiedener pitch classes zu einer Menge. Eine solche Sammlung kann aus gleichzeitig oder auch nacheinander erklingenden Tönen gebildet werden. Sie entspricht im Wesentlichen dem Begriff „Akkord“ oder besser „Harmonie“ der herkömmlichen Harmonielehre. Ein Set beinhaltet also sinnvollerweise die Klassen von pitches, die als zusammengehörig betrachtet werden. Manchmal begegnet man auch dem synonym gebrauchten Begriff pitch class collection. Ein Set kann aus 2 bis 12 pitch classes bestehen (mehr gibt es ja nicht in der chromatischen Skala), wobei letzteres Set auch als aggregate (=dt. Menge, Gesamtheit) bezeichnet wird, da es alle der Theorie nach existenten pitches (nämlich die chromatischen Halbtöne) enthält.
Für die schriftliche Darstellung eines p. c. sets gibt es, um eine optimale Vergleichbarkeit zu gewährleisten, bestimmte Konventionen. Eine davon, die sogenannte integer notation, besagt, dass jedes pitch durch eine Ganzzahl dargestellt werden soll, indem man einem Referenzton (in der Regel ist dies das c, theoretisch ist aber jeder andere Ton genauso möglich!) den Wert „0“ zuweist und alle folgenden Halbtöne der chromatischen Skala einfach ab „1“ aufsteigend durchnummeriert. Die Werte der pitches eines Sets werden dann, durch Kommata getrennt, in runden Klammern angegeben. So ließe sich z. B. ein c-Moll-Dreiklang durch das Set (0,3,7) darstellen. „0“ für das c, „3“ für das es (3 Halbtöne über dem c), „7“ für das g (7 Halbtöne über dem c). Aber auch ein f-Moll-Dreiklang könnte durch (0,3,7) ausgedrückt werden, da jedes Set zur besseren Vergleichbarkeit auf den Ursprung „0“ (in unserem Falle also das c) transponiert werden sollte. Eine weitere Konvention besagt, dass ein Set die enthaltenen pitches auch von oben nach unten gelesen darstellen kann. Schreitet man vom c nun einmal 3 und einmal 7 Halbtöne abwärts, ist das Resultat ein F-Dur-Dreiklang, und man wird sehr schnell feststellen, dass durch das Set (0,3,7) nicht nur der grundstellige c-Moll-Dreiklang, sondern sämtliche Dur- und Moll-Dreiklänge in allen Lagen und – wie im Folgenden noch gezeigt werden wird – Umkehrungen repräsentiert werden. Das Set gibt also lediglich an, dass es sich um 3 verschiedene pitch classes handelt, die, in eine beliebige Richtung gelesen, die Intervallabstände von ip3 (von „0“ zu „3“) und ip4 (von „3“ zu „7“) haben. Um nun vom Notentext auf ein zugrunde liegendes Set zu gelangen, das noch dazu so eindeutig dargestellt werden kann, dass ein Vergleich mit anderen Sets nicht zu mühevoller mathematischer Knochenarbeit wird, gibt es mehrere Wege, sowohl mathematischer Natur, als auch durch Überlegungen am Notentext. Im Folgenden wird eine mögliche Verfahrensweise vorgestellt, die sich sehr schnell bewerkstelligen lässt und relativ fehlerunanfällig ist.
normal order
Unter normal order versteht man diejenige Anordnung eines p. c. sets, bei der die äußeren beiden Vertreter das kleinstmögliche Intervall bilden. Dies lässt sich am bequemsten durch folgende drei Arbeitsschritte bewerkstelligen (als Beispiel dient hier ein Ausschnitt aus der Stimme der ersten Klarinette zu Beginn von A. Schönbergs Op. 6,5):

In manchen Fällen kommt dieses größte Intervall mehr als einmal vor, dann gibt es zwei oder mehr Varianten der normal order, die alle bei den weiteren Berechnungen berücksichtigt werden müssen.
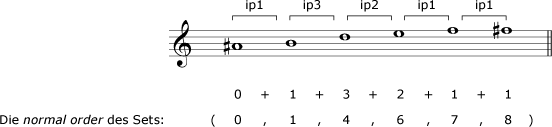
Um das Schönberg-Set mit „0“ beginnen zu lassen, gibt es jetzt zwei Möglichkeiten: man transponiert alle Töne so, dass der erste ein c ist, was jedoch leicht zu Fehlern führen könnte. Besser ist vielleicht, den Referenzton vom c auf das ais zu verlegen, dann beginnt die obige normal order bereits mit „0“. Wenn man sich nun noch zwischen zwei Noten die jeweiligen pitch intervals notiert, braucht man diese nur noch der Reihe nach aufzuaddieren und nach der Null in die Mengenklammer einzutragen:
best normal order und prime form
Die oben ermittelte normal order ist nicht der alleinige Repräsentant dieses Sets, denn, wie bereits erwähnt, kann ein Set auch rückwärts gelesen, bzw. die Intervalle des Sets vom Referenzton abwärts gebildet werden. Dieser Vorgang heißt Umkehrung oder inversion. Um die inversion dieses Sets zu bilden, können nun die pitch intervals von rechts nach links aufaddiert werden, ausgehend von fis als pitch mit dem Wert „0“, oder aber man löst dies auf mathematischen Wege, indem man einfach die Menge der normal order rückwärts schreibt und von der höchsten Zahl (also der letzten Zahl der normal order) subtrahiert:
inversion von ( 0 , 1 , 4 , 6 , 7 , 8 ) = ( 8 – 8 , 8 – 7 , 8 – 6 , 8 – 4 , 8 – 1 , 8 – 0 ) = ( 0 , 1 , 2 , 4 , 7 , 8 )
Als best normal order bezeichnet man die Version eines Sets (inklusive aller möglichen Transpositionen und Umkehrungen), das von dem kleinstmöglichen Intervall umschlossen wird und mit den kleinstmöglichen Intervallen beginnt. Das heißt: Die oben gebildete Umkehrung (0,1,2,4,7,8) hat – von links nach rechts gelesen – kleinere Intervalle zu Beginn als die ursprüngliche normal order (0,1,4,6,7,8) und ist somit eine better normal order oder, da es in diesem Falle nur zwei normal orders gibt, die best normal order. Die best normal order repräsentiert zugleich immer auch die prime form (=dt. „Primärgestalt“) eines pitch class sets. Der Unterschied zwischen den Begriffen best normal order und prime form besteht eigentlich nur darin, dass erster die Gestalt des Sets in pitches oder Tönen ausdrückt, während letzter die Gestalt in Zahlen verkörpert. Allan Forte hat die für die musikalische Analyse relevanten prime forms zusammengestellt und systematisiert. Das Schönberg-Set hat demnach den Namen „6-Z17“, welcher in folgende Bestandteile zerlegt werden kann: Die erste Zahl („6“) gibt die Kardinalität des Sets, d. h. die Anzahl der Elemente (sprich: pitch classes) in dieser Menge an; die zweite Zahl („17“) ist die Ordnungszahl, die bei der Nummerierung auf dieses Set gefallen ist, und das vorangestellte „Z“, welches bei den meisten Set-Namen fehlt, deutet auf eine Besonderheit dieses Sets hin, auf die im folgenden Abschnitt noch näher eingegangen wird.
interval vector oder interval class vector (i. c. vector)
Die weiter oben angesprochenen 6 interval classes finden nun, da die prime form des Sets ermittelt ist, endlich ihre Anwendung: Von jeder prime form lässt sich ein so genannter interval (class) vector ableiten, der anzeigt, wie oft jede dieser 6 interval classes in einem Set vorkommt. Aus diesem Grund beinhaltet der Intervallvektor auch genau 6 Werte, umschlossen von eckigen Klammern. Um den interval vector zu ermitteln, muss jedes Element eines Sets auf Basis der interval classes miteinander verglichen werden. In einem Set aus sechs Elementen müssen also 5 + 4 + 3 + 2 + 1 = 15 Intervalle berechnet werden. Diese alle am Notentext zu ermitteln, wäre sehr aufwändig und unübersichtlich, sodass auch hier wieder der mathematische Weg als der sinnvollere erscheint: Man subtrahiert von jedem Element eines Sets sämtliche kleineren Werte, ausgehend vom größten Wert. In anderen Worten: Man fängt mit der Zahl ganz rechts an, subtrahiert von ihr alle Zahlen, die links von ihr stehen, und schreibt das Ergebnis in eine Tabelle mit den Spalten von 1 bis 11. Da das größte Intervall des Schönberg-Sets aus 8 Halbtönen besteht, bleiben die letzten drei Spalten leer. Das Intervall mit 6 Halbtonschritten ist der Tritonus und somit die Teilung der Oktave, demnach sind alle Intervalle mit mehr als 6 Halbtonschritten Komplementärintervalle der ersten fünf, und zwar in spiegelverkehrter Reihenfolge. In anderen Worten: Wenn ein Intervall n Halbtonschritte umfasst, hat sein Komplementärintervall 12 – n Halbtonschritte, und beide sind Instanzen derselben Intervallklasse:

Der diesem Set zu Grunde liegende interval vector ist also [322332], das bedeutet, es sind 3 Instanzen der i. c. 1 im Set enthalten, 2 Instanzen der i. c. 2, usw.
Viele pitch class sets haben einen ihnen eigenen, einmaligen interval vector. Es gibt jedoch Sets, die sich in ihrer prime form zwar voneinander unterscheiden, jedoch einen identischen Intervallvektor besitzen. Diese Art der Verwandtschaft wird Z-relation genannt, man spricht von Z-related p. c. sets oder Z-mates. Allan Forte arbeitete diese Besonderheit in seine Nomenklatur ein, indem er in den Set-Namen ein „Z“ vor die Ordinalzahl stellte. Das Beispiel-Set von Schönberg (6-Z17) z. B. ist Z-related mit dem Set 6-Z43, welches zwar eine andere prime form, nämlich (0,1,2,5,6,8), aber denselben interval vector [322332] hat.
Hinweise
Anschließend sei noch bemerkt, dass die Schreibweisen in der p. c. set theory bei verschiedenen Autoren zum Teil von einander abweichen. Statt der Literale „10“ oder „11“ in der prime form findet man bisweilen „T“ („ten“) bzw. „E“ („eleven“), oder auch „A“ bzw. „B“ als Anlehnung an die Schreibweise im hexadezimalen Zahlensystem. Außerdem begegnet man mitunter statt runder auch eckigen Klammern bei Angaben einer normal order bzw. prime form, und Intervallvektoren werden gelegentlich auch mit Kommata zwischen den Zahlen geschrieben.[3]
Auch zur Ermittlung der prime form gibt es verschiedene Verfahrensweisen. Rahn berechnet, im Gegensatz zu Forte, die prime form derart, dass die kleineren Intervalle von rechts gelesen erscheinen. Dies wirkt sich allerdings nur in insgesamt sechs Sets aus:
| Forte-Name | prime form nach Forte | prime form nach Rahn |
|---|---|---|
| 5-20 | (0,1,3,7,8) | (0,1,5,6,8) |
| 6-31 | (0,1,3,5,8,9) | (0,1,4,5,7,9) |
| 6-Z29 | (0,1,3,6,8,9) | (0,2,3,6,7,9) |
| 7-Z18 | (0,1,2,3,5,8,9) | (0,1,4,5,6,7,9) |
| 7-20 | (0,1,2,4,7,8,9) | (0,1,2,5,6,7,9) |
| 8-26 | (0,1,2,4,5,7,9,A) | (0,1,3,4,5,7,8,A) |
[1] Forte, Allan (1973), The Structure Of Atonal Music, New Haven: Yale University Press.
[2] Rahn, John (1980), Basic Atonal Theory, MacMillan Publishing Company.
[3] Der Gebrauch von Kommata ist vor allem dann sinnvoll, wenn zweistellige Ziffern in Intervallvektoren notiert werden müssen. Dies ist bei lediglich zwei Sets der Fall, nämlich dem elftönigen und zwölftönigen Set (Aggregat). Hier verwendet man jedoch eher die Buchstaben „A“, „B“ und „C“ statt der Zahlen „10“, „11“ und „12“.
Erstellung des Beitrags: 7. April 2013
Letzte Änderung des Beitrags am 10. Juni 2014