Analysemethoden (Pop/Rock) – Ein Überblick
Einführung
Dieses Tutorial dient dem Überblick, welche Methoden in aktuellen Publikationen zur Analyse von Popularmusik verwendet werden. Am Ende des Tutorials finden Sie Literaturhinweise zu ausgewählten Themen.
Inhalt:
Funktionstheorie − Stufentheorie − grafische Analysen (nach H. Schenker) − Satzmodelle − Forensische Analyse − Music Cognition
Funktionstheorie
Die Funktionstheorie ist eine in Deutschland teilweise noch gebräuchliche Methode zum Chiffrieren harmonischer Verläufe. Begründer der Funktionstheorie war Hugo Riemann (1849−1919, weitere Informationen zur Funktionstheorie finden Sie hier). Das folgende Beispiel zeigt eine harmonische Analyse der Basslinie des Songs A Whiter Shade Of Pale (1967) der Band Procol Harum:
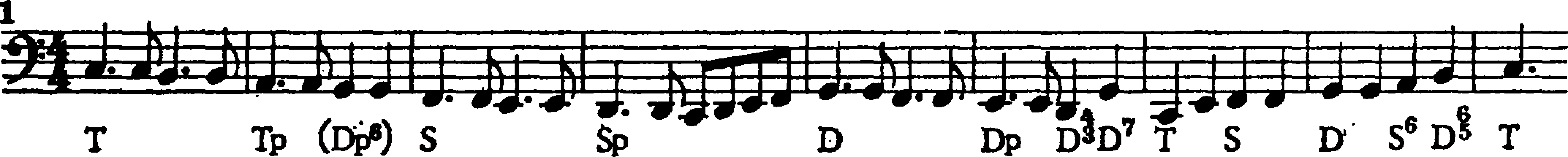
Manfred Schuler, »Rockmusik und Kunstmusik der Vergangenheit. Ein analytischer Versuch«, in: Archiv für Musikwissenschaft 35 (1978), S. 135‐150. Quelle der Sounddatei: YouTube.
Manfred Schuler (1931−2001) war Musikwissenschaftler und Musikpädagoge, der Kirchen- und Schulmusik sowie Musikwissenschaften in Freiburg im Breisgau und München studierte hatte (u.a. bei W. Gurlitt und Thr. Georgiades). 1982 erhielt er eine Professur für Musikerziehung und Didaktik in Mainz.
Auch in dem Aufsatz »Musikalische Analyse und Sound« von Heinz Bamberg wird die Funktionstheorie zur harmonischen Chiffrierung im Rahmen eines Songvergleichs verwendet:

Heinz Bamberg, »Musikalische Analyse und Sound«, in: Beiträge zur Popularmusikforschung 07/08 (1989), S. 84‐92, URN: urn:nbn:de:hebis:26‐opus‐53300«.
Die Aufsätze von Schuler und Bamberg stammen aus den 1970er und 1980er Jahren, also aus einer Zeit, in der die Verwendung der Funktionstheorie in der deutschsprachigen Musikwissenschaft verbreitet war. In aktuellen Publikationen ist das Verwenden von Funktionssymbolen zur harmonische Analyse dagegen unüblich.
Stufentheorie
Das Verwenden von Stufenzeichen zur Chiffrierung harmonischer Verläufe ist in Analysen zur Popularmusik hingegen verbreitet (mehr zur Entwicklung der Stufentheorie finden Sie hier). In seinem Aufsatz »Form in Rock Music. A Primer« verwendet John Covach im Rahmen von Formanalysen eine sehr ökonomische Art zur Chiffrierung harmonischer Verläufe, indem er arabische Zahlen (für die Anzahl von Takten) mit Kleinbuchstaben kombiniert. Im Fußbereich einer Formanalyse befindet sich dann eine Legende:

John Covach, »Form in Rock Music. A Primer«, in: Engaging Music. Essays in Music Analysis, New York 2005, S. 65–76. Quelle der Sounddatei: YouTube.
Bitte beachten Sie, dass in englischsprachigen Publikationen zur Popularmusik im Gegensatz zu deutschsprachigen großen arabischen Ziffern für Dur-Akkorde (z.B. I IV V I) und kleine für Moll-Akkorde (z.B. ii, iii und vi) verwendet werden.
Grafische Analyse (nach H. Schenker)
Insbesondere in nordamerikanischen Publikationen zur Popularmusik sind sogenannte ›Schenker-Analysen‹, also grafische Analysen nach Heinrich Schenker verbreitet:

Anfang der Analyse (Verse) von Walter Everett, The Beatles as Musicians. The Quarry Men through Rubber Soul, New York 2001, S. 199. Quelle der Sounddatei: YouTube.
Ein Vorteil dieser Analysemethode besteht darin, dass in grafischen Analysen nach Schenker grundsätzlich kein Rhythmus notiert wird (die Notenlängen kennzeichnen in grafischen Analysen die strukturelle Bedeutung von Tonhöhen an und nicht eine spezifische Länge). Das Fehlen des Parameters Rhythmus erweist sich insofern als Vorteil, weil das Mikrotiming in Popularmusik einer klassischen Notation tendenziell entgegensteht und deswegen in der Regel in Transkriptionen auch nur näherungsweise gelingt. Zur Chiffrierung der Harmonik werden in grafischen Analysen nach H. Schenker die Stufensymbole (s.o.) verwendet.
Satzmodelle
Als Satzmodelle werden ›Satztypen und -formeln des 15. und 16. Jahrhunderts‹ bezeichnet, auf die der Musikwissenschaftler Carl Dahlhaus in seiner Habilitationsschrift hingewiesen hat. Die klassischen Satzmodelle sind dabei in vielen Fällen hervorragend geeignet, sowohl melodisch-harmonische Zusammenhänge zu veranschaulichen. Zum Beispiel lässt sich der Verse von »I Want To Hold Your Hand« von The Beatles nicht nur über die I-III-V-I- und I-IV-V-I-Kadenzharmonik verstehen, die Walter Everett in der Analyse oben als Wesentlich erachtet hat, sondern auch über das Satzmodell des Parallelismus, wie es das nachfolgende Diagramm zeigt:

Alternative Interpretation zu »I Want to Hold Your Hand« von The Beatles, die das Satzmodell des Parallelismus in den Vordergrund rückt.
Forensische Analyse
Helmut Rösing schrieb über die Forensische Popmusik-Analyse:
Forensische Popmusik-Analyse ist immer vergleichend. Ausgangspunkt sind zwei Musikstücke: ein urheberrechtlich geschütztes Original udn ein später entstandenes Stück, in dem angeblich urheberrechtlich geschütztes Material Verwendung gefunden hat. Was der Kläger diesbezüglich vorbringt, versucht die Seite der Beklagten zu widerlegen.
Die Argumentation des Klägers vollzieht sich in der Regel in zwei Schritten, um eine Urheberrechtsverletzung so plausibel wie möglich nachzuweisen. Erstens muss deutlich gemacht werden, dass das Originalwerk eine eigenschöpferische Qualität und Wertigkeit besitzt. Grundlage dafür ist die minutiöse Analyse kleinster Musikpartikel, die aus kunstmusikalischer Sicht als eher trivial oder banal abgetan zu werden pflegen, hier aber als Indikatoren für musikalische Prägnanz stehen: Aus musikstrukturellen ›Kleinigkeiten‹ kann eine Motivsemantik erwachsen, die für geistiges Eigentum kennzeichnend ist [...]
Die Abwehrstrategie der Beklagtenseite besteht darin, diese Eigentümlichkeiten klein zu reden. Als Beleg wird gerne auf die Nähe zu volkstümlichem und damit urheberrechtsfreiem Liedgut verwiesen. Oder aber auf angeblich vergleichbare Partien aus so genannten klassischen Kompositionen. Im Vergleich mit deren Strukturen wird dann die Machart des Poptitels als banale Anwendung rein handwerklicher Musikbetätigung abgetan.
Helmut Rösing, »Forensische Popmusik-Analyse«, in: Black Box Pop, Bielefeld 2012, S. 257-258
Selbst dann, wenn man Helmut Rösing in seiner Diagnose über das Wesen der Pop-Rockmusik nicht folgen mag, weil diese einem veralteten Musiktheorie-Verständnis verpflichtet ist und die eigene Beobachter-Position nicht angemessen reflektiert, sind seine Erläuterungen zur Forensische Popmusik-Analyse präzise und getragen von reichen Erfahrungen in diesem Bereich. Als Methoden verwendet Rösing in seinem Aufsatz vergleichende Transkriptionen (und bedient sich damit sehr konventionellen Methoden der musikalischen Analyse) sowie technische Verfahren zur Soundanalyse (unter Zuhilfenahme einschlägiger Audio-Software).
Temperleys Scalar Shift
David Temperley beobachtet Musik aus der Perspektive der Kognitionsiwssenschaften und versucht Preference-Rules für die Wahrnehmung von Musik zu bestimmen. Zum Beispiel lautet die erste Well formed Definition zur Harmonischen Struktur eines Stückes: »«A well-formed harmonic structure is a complete segemntation of a piece into non-overlapping chord-spans«. Hinzu kommen zahlreiche Hypothesen wie z.B. »The function of a chord is arbitrarily related to the pitches that comprise it«, »The functions of a motive are arbitrarily related to the pitches that comprise it« und »The meaning of a musical schema is arbitrarily related to the form: the notes and infrastructural elements that comprise it«.
Annahmen dieser Art identifizieren die Funktion von Elementen mit ihrem musikalischen Material und da sich musikalische Parameter mit der Computer erforschen lassen, ist Temperleys Forschungsansatz als »computational modeling of music cognition« bekannt geworden.
Ohne auf den Ansatz Temperleys näher einzugehen, der stark von der von Fred Lerdahl (Komponist und Musiktehoretiker) und Ray Jackendoff (Linguist) 1983 publizierten Generative Theory of tonal Music (GTTM) beeinflusst ist, sei hier eine seiner Methoden exemplarisch erwähnt. In seinem Aufsatz »Scalar Shift in Popular Music« beschreibt Temperley einen sogenannten scalar shift:
The idea is simple: The scale-degree content of a song (or a section of a song) tends to occupy a certain region on the “line of fifths,” the circle of fifths stretched out infinitely in both directions. Moving outside this region—especially if the move is emphasized (by rhythmic, textural, or other means) and involves multiple pitch classes—creates a sense of scalar shift. Such shifts may be momentary, as in the case of “Then Came You”; in other cases, they may be longer in duration, and may play a role in defining the large-scale formal structure of the song. I will argue, also, that scalar shifts often have interesting expressive implications—sometimes simply indicating a change in mood or situation, and sometimes carrying more specific emotional connotations, analogous to the expressive meanings of major and minor in common-practice music.
Temperley 2011, Scalar Shift in Popular Music.
Die folgende Abbildung zeigt die Line-of-fifths representation in dem Song »A Hard Day’s Night« von The Beatles (Lennon/McCartney):
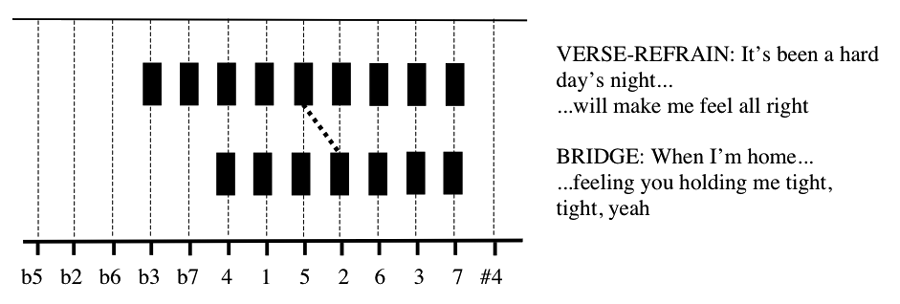
Abbildung aus: David Temperley, »Scalar Shift in Popular Music«, in: MTO 4/2011.
Ohne Temperley im Speziellen darin folgen zu wollen, einen scalar shift in Popularmusik auf den Textinhalt zu beziehen, so lassen sich nicht selten besondere Klangwirkungen über eine Veränderung des Tonmaterials erklären und über einen Quintenturm veranschaulichen.
Bitte haben Sie einen Moment Geduld, bald geht es hier weiter...
Erstellung des Beitrags: 6. April 2020
Letzte Änderung des Beitrags am 6. April 2020