Analysemethoden – Ein Überblick

von Ulrich Kaiser

Einführung

Dieses Tutorial ist als Einstieg gedacht, wenn Sie Interesse an den verschiedenen Methoden haben, die zur strukturellen Analyse von Musik verwendet werden. Am Ende des Tutorials finden Sie darüber hinaus interne und externe Links für weiterführende Anleitungen zu den jeweiligen Themen.

Inhalt:
Funktionstheorie − Stufentheorie − Generalbass − Oktavregel − Fundamentalbass − Kontrapunkt − Gliederungsanalysen über Kadenzen − Graphische Analyse − Pc-set Analyse − Satzmodelle − Energetische/dynamische Analyse − Soundanalyse − GTTM − Tonfeld-Analyse − Literatur

Funktionstheorie

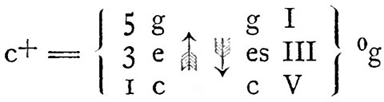
Begründer der Funktionstheorie war Hugo Riemann (1849−1919). Allerdings sahen seine Zeichen zur Chiffrierung harmonischer Verläufe noch ganz anders aus als die heute gebräuchlichen Funktionssymbole. Das lag vor allen Dingen daran, dass Riemann ein sogenannter Dualist war, das heißt: Riemann ging davon aus, dass die harmonische Logik in Dur durch die Obertonreihe, in Moll durch eine Untertonreihe bestimmt wird. Die Basis des C-Dur-Dreiklangs wäre demnach C (der C-Dur-Dreiklang kommt in der Obertonreihe als 4., 5. und 6. Oberton vor), die Basis des c-Moll-Dreiklangs jedoch g (gedacht über eine spiegelbildlich zur Obertonreihe konstruierte Untertonreihe):

Die folgende Abbildung zeigt die Buchstabenchiffrierung, wie sie Riemann 1898 am Schluss seiner Geschichte der Musiktheorie dargelegt und zu den Stufenzeichen Gottfried Webers in Beziehung gesetzt hat:

Die Funktionszeichen hat Riemann eingeführt, um die harmonische Analyse zu vereinfachen: Einerseits wollte er dasselbe Zeichen für die verschiedenen Akkordumkehrungen verwenden können (an der Chiffrierung der Umkehrungen eines Dominantseptakkords im Generalbass störten ihn die vier verschiedenen Bezifferungen 7 / 5-6 / 3-4 und 2-4), andererseits durch Verallgemeinerung die »Loslösung der Bezeichnung von der einzelnen Tonart« erreichen. Wie schon bei der Buchstabenchiffrierung lässt sich jedoch auch an Riemanns Funktionszeichen das dualistische Denken erkennen (die o vor den Funktionszeichen in Moll):

Viele Autoren wie Max Reger und Hermann Grabner haben sich im Anschluss an Riemanns Publikationen um eine weitere Vereinfachung der Funktionstheorie bemüht. In Deutschland durchgesetzt hat sie sich über die dritte Auflage der der Harmonielehre Wilhelm Malers (Beitrag zur Harmonielehre, unter Mitarbeit von Günter Bialas und Johannes Driessler entstanden). Hier zeigt sich die Funktionstheorie vom Dualismus weitgehend bereinigt. Ab der vierten Auflage hieß die schmale Publikation dann übrigens Beitrag zur Durmolltonalen Harmonielehre.
Die Funktionstheorie wurde dann von Mahlers Schüler Diether de la Motte (1928−2010) weiterentwickelt. Seine wirkungsmächtigen Taschenbücher festigten die Vormachtstellung der Funktionstheorie in Deutschland (insbesondere über die Bücher Harmonielehre, 1976 und Kontrapunkt, 1981). Prominenter Schüler von Diether de la Motte war Clemens Kühn (* 1945), der ebenfalls in seinen weit verbreiteten Publikationen die Funktionstheorie bevorzugt verwendet hat. Die folgende Tabelle gibt einen Überblick über heute gebräuchliche Symbole der Funktionstheorie:

Da zu der Funktionstheorie in ihrer aktuellen Ausprägung gehören keine Aussagesätze mehr, die regulieren würden, welche Harmonien aufeinander folgen dürfen und welche nicht (wie z.B. »einer V. Stufe darf keine IV. Stufe folgen«). Daher ist die Funktionstheorie im wissenschaftstheoretischen Sinn keine Theorie, sondern eine Methode (zur Chiffrierung von Akkorden).

Tutorials auf musikanalyse.net zur Funktionstheorie:

• Sequenzen und die Funktionstheorie

Stufentheorie

Historisch älter als die Funktionstheorie sind Stufenzeichen, die bereits Johann Philipp Kirnberger (1721−1783) und Georg Joseph Vogler (1749−1814) verwendeten. Weiterentwickelt und systematisch verwendet wurden die Stufenzeichen von Gottfried Weber (1779−1839), der heute als Begründer der Stufentheorie gilt. In der Stufentheorie werden die Tonstufen der Tonart mit römischen Ziffern gekennzeichnet. Große Ziffern symbolisieren Durakkorde, kleine Ziffern Mollakkorde. Der verminderte Dreiklang wird durch ein kleines Kreissymbol gekennzeichnet (nicht zu verwechseln mit dem Kreissymbol des ›Dualisten‹ Riemann), der übermäßige Dreiklang durch ein Kreuz oder einen kleinen Strich. Als Ziffer rechts neben dem Stufensymbol war anfangs nur die 7 gebräuchlich, chromatische Veränderungen wurden durch ein # oder b angezeigt (wie im Generalbass). Ernst Friedrich Richter verwendete zusätzlich zu den Stufenzeichen Generalbassziffern für die Akkordumkehrungen, die dann später auch rechts neben den Stufenziffern notiert wurden. Die folgende Tabelle gibt eine Übersicht über die gebräuchlichen Stufenzeichen:

Die Verwendung von Stufenzeichen ist heute insbesondere noch in der Analyse von Pop- und Rockmusik gebräuchlich. Problematisch ist, dass es gerade in diesem Bereich nicht selten Harmoniepattern gibt, bei denen sich eine I oder i nicht ohne Willkür festlegen lässt. Zum Beispiel ist es sowohl angemessen, das gängige Pattern Am - F - C -G als i - VI - III - bVII als auch als vi - IV - I - V zu zu chiffrieren (da die Hörweise wechseln kann, je nachdem, ob das Pattern einmal oder mehrmals hintereinander erklingt).
Auch der Stufentheorie fehlen Aussagesätze, die regulieren würden, welche Harmonien aufeinander folgen dürfen und welche nicht (wie z.B. »nach einer V. Stufe darf keine IV. Stufe folgen«). Daher ist die Stufentheorie wie schon die Funktionstheorie keine Theorie im wissenschaftstheoretischen Sinn, sondern eine Methode (zur Chiffrierung von Akkorden).

Tutorials auf musikanalyse.net zur Stufentheorie gibt es derzeit noch nicht.

Generalbass

Der Generalbass entwickelte sich um 1600 mit dem Ziel, nur anhand einer Bassstimme ad-hoc den harmonischen Verlauf einer Komposition darstellen zu können. Harmonische Mehrdeutigkeiten im Zusammenhang mit einem Basston wurde durch Ziffern geklärt (früher meist über, heute in der Regel unter den Noten der Bassstimme). Die Ziffern im Generalbass geben an, welche Intervalle zu einem Basston (nicht zum Grundton) zu greifen sind. Leitereigene Dreiklänge in ihrer Grundstellung bleiben dabei unbeziffert (die Ziffern 3 und 5 werden nur in Ausnahmefällen notiert), Alterationen von Tönen werden neben die entsprechende Ziffer gesetzt (z.B. 4# oder 2b). Selbstverständliche Ziffern bzw. Ziffern, die sich aus dem Zusammenhang erschließen lassen, wurden nicht notiert wie z.B. die 3 in einem Sextakkord oder die 6 in einem Sekundakkord. Für alterierte kleine und große Terzen findet man in frühen Quellen häufig ein b und #. Ein b unter einem a-Moll Akkord wies den Spieler darauf hin, dass die Terz den Charakter einer b-Note (also einen fa-Charakter) bzw. den Halbton unter sich und den Ganzton über sich haben sollte (der Akkord a-ces-e war im 17. und 18. Jahrhundert musikalisch unsinnig). Heute wird für die Alteration von Terzen auch das Auflösungzeichen verwendet. Erhöhungen bestimmter Töne wurden zudem häufig über durchstrichene Ziffern angezeigt (z.B. eine durchgestrichene 2, 4 oder 6 steht für 2#, 4# oder 6#, eine vergleichbare Kurzschrift für erniedrigte Töne gibt es nicht). Im 18. Jahrhundert fanden des Weiteren waagerechte Striche für das Liegenbleiben von Harmonien Verwendung. Die folgenden Abbildung zeigt eine Tabelle aus der Kleine[n] General=Bass=Schule von Johann Mattheson (Hamburg 1734) zu den bekannten (und sogar »ungewöhnlichen‹) Ziffern:

Im theoretischen Sinn versteht man unter dem Terminus Generalbass also eine Methode zur Kennzeichnung eines harmonischen Verlaufs mithilfe von Ziffern. Eine Theorie im wissenschaftstheoretischen Sinn verbindet sich mit der Generalbassnotation nicht.

Tutorials auf musikanalyse.net zur Funktionstheorie:

• Der Generalbass. Eine interaktive Einführung

Eine Einführung in die Generalbassbezifferung sowie ein interaktives Tool zum Üben der gebräuchlichsten Generalbassziffern finden Sie hier.

Oktavregel

Hinter dem Begriff Oktavregel verbirgt sich eine Praxis, mit der im 17. und 18. Jahrhundert das Komponieren erlernt sowie der Umgang mit unbezifferten Basstimmen geübt worden ist. Die Oktavregel gibt dabei vor, mit welchen Harmonien die Töne einer Tonart im Bass zu harmonisieren sind.

Während sich mit der Funktionstheorie, der Stufentheorie oder auch dem Generalbass alle denkbaren Harmonien chiffrieren lassen, ohne dass bestimmte Akkordwendungen theoretisch ausgeschlossen würden, gibt die Oktavregel in hohem Maße vor, wie ein Basston zu harmonisieren ist. Beispielsweise ist nach der Oktavregel ein e im Bass in C-Dur immer Träger eines C-Dur-Sextakkords. Die Harmonisierungen des e als E-Moll-Grund- oder a-Moll-Quartsextakkords (oder anderer Harmonisierungen) scheiden nach der Okatvregel aus. Aufgrund dieser Selektionsleistung könnte man in der Oktavregel nicht nur eine Methode, sondern auch eine − zugegebener Maßen ganz elementare − Theorie ansehen, deren Handleitungen auch als Aussagesätze formuliert werden könnten wie zum Beispiel: »In C-Dur muss jedes e im Bass Teil einer C-Dur-Harmonie sein« (wobei sich dieser Satz dann als wahr oder unwahr erweisen kann).

Tutorials auf musikanalyse.net zur Oktavregel:

• Die Oktavregel (Regola dell'ottava)

Fundamentalbass

Der Fundamentalbass (bzw. franz. Basse fondamentale) geht zurück auf den französischen Komponisten und Musiktheoretiker Jean-Philippe Rameau. Die Rameaurezeption in Deutschland erfolgte in erster Linie über Kirnberger und Marpurg. Marpurg schrieb über die Basse fondamentale Rameaus:

In MArpurgs Sinne ist der Grundbass nicht viel mehr als ein didaktisches Hilfsmittel, sich die Grundstellungen von Akkorden im Generalbass besser verdeutlichen zu können. Viele Komponisten wie zum Beispiel Wolfgang Amadeus Mozart dürften dieses Verständnis eines Fundamentbasses – der nur gedacht und nicht gehört werden sollte – im 18. Jahrhundert geteilt haben. Das war allerdings ursprünglich nicht die Absicht Rameaus, der in der Basse fondamentale mehr sah als ein nachträgliches Huilfsmittel zur Veranschaulichung von Akkordverbindungen.
Ausgangspunkt Rameaus ist die Auffassung, dass alle harmonischen Ereignisse sich auf Dreiklänge und Septakkorde zurückführen lassen. Diese Akkorde hätten eine »Centre harmonique«, ein harmonisches Zentrum bzw. einen Grundton, wobei die Grundtöne der Akkorde eine (gedachte) Stimme bilden, die vom realen Bass bzw. Klangeschehen unabhängig ist. Diese Stimme nannte Rameau Basse fondamentale, in der Basse fondamentale sah er die verborgene Grundlage aller harmonischen Progressionen. Die folgende Abbildung zeigt Rameaus Interpretation der Oktavregel:

Für Rameau entstand allerdings ein musikalischer Zusammenhang erst durch die Wechselwirkung von Dissonanzauflösung, Fundamentschritt und Akkordbdeutung. Das Zusammentreffen beispielsweise einer abwärtsführenden Septimauflösung mit einem Quintfall (Dominante) oder einer aufwärtsführenden Sixte-ajoutée-Auflösung mit einem Quartfall im Fundament verlieh zwei Tonleiterstufen eine spezifische Bedeutung im Rahmen einer Tonart. Und harmonische Bewegungen konnten nach Rameau so lange durch Dissonanzauflösungen und Funamentschritte weiter entwickelt werden, bis ein dissonanzloser Accord perfait die Komposition beendet.
Heute wird unter dem Begriff Fundamentalbass zwar noch die (gedachte) Stimme verstanden, die aus Grundtönen von Akkorde besteht. Die Bedeutung, die Rameau seinerzeit der Dissonanz zumaß, wird jedoch in der Regel vernachlässigt.

Tutorials auf musikanalyse.net zum Fundamentalbass gibt es derzeit nicht.

Kontrapunkt

Bitte haben Sie einen Moment Geduld, bald geht es hier weiter...