Schenker reloaded - Graphische Analysen nach Heinrich Schenker
In diesem Tutorial wird eine musikalische Analysemethode vorgestellt, die auf den Musiktheoretiker Heinrich Schenker zurückgeht, der in Wien zwischen 1884 und 1935 gelebt und unterrichtet hat. Schenkers Analysemethode wird auch als graphische Analyse, Reduktionsanalyse oder Schichtenlehre bezeichnet. Während der Ausdruck Reduktionsanalyse eigentlich auf jede Form musikalischer Analyse zutrifft, ist der Ausdruck Schichtenlehre treffend, weil Schenker davon ausging, dass es in der Musik Schichten gibt (Vorder-, Mittel- und Hintergrund), die sich wechselseitig beeinflussen. Interessant ist, dass zeitgleich und ebenfalls in Wien von Sigmund Freud eine Schichtenlehre für das menschliche Bewusstsein formuliert worden ist (bewusst, vorbewusst und unbewusst). Martin Eybl hat darauf hingewiesen, dass die Denkfigur einer verborgenen Ordnung (Hintergrund / Unbewusstes) auch Ausdruck eines Zeitgeistes einer intellektuellen Elite Wiens auf das Zerbrechen politischer und kultureller Systeme um die Jahrhundertwende gewesen sein könnte.
Graphische Analysen werden in Deutschland kaum, in Amerika hingegen sehr häufig verwendet. Die Gründe hierfür könnten darin liegen (vgl. hierzu auch den Abschnitt Widerstände), dass Schenker 1935 gestorben ist, er Jude und seine Theorie während der Naziherrschaft folglich chancenlos war. Felix Salzer, ein Schüler und überzeugter Anhänger Heinrich Schenkers, emigrierte 1939 nach Amerika, lehrte dort an einflussreichen Institutionen und hinterließ zahlreiche Publikationen. Im Gegensatz zu seinem Lehrer setzte Salzer graphische Analysen auch für Musik des 20. Jahrhunderts ein und gab damit einen Impuls, der zur ihrer Verwendung in der nordamerikanischen Popularmusikforschung geführt hat.
Inhalt:
- Wozu Schenker?
- Die Sonate ›facile‹ KV 545 von W. A. Mozart als Beispiel
- Der Hauptsatz. in Schichten zerlegt...
- Die Schichten der Überleitung
- Die Schichten des Seitensatzes
- Die Schichten der Schlussgruppe
- Schenkers Analysen
- Formfunktionen und strukturelle Einheit
- Angemessenheit und didaktische Dimension
- Widerstände und Perspektiven
- Literatur & Weblinks
Wozu Schenker?
Wenn man im Konzert eine Beethoven-Sinfonie hört, kann man einen Punkt wahrnehmen, an dem man weiß, dass die Sinfonie bald zu Ende sein wird. Und das, obwohl die Komposition anschließend oft noch ein paar Minuten lang dauert. Wie ist es möglich, dass man beim Hören von Musik in die Zukunft hören kann? Diese spannende musiktheoretische Frage lässt sich leider nicht alleine über Kontrapunkt und Harmonielehre beantworten, weder Chiffrierungssysteme der Funktions- oder Stufentheorie noch Satzmodell-Analysen können uns auf diese Frage eine befriedigende Antwort geben. Eine graphische Analyse nach Heinrich Schenker hingegen schon...
Darüber hinaus gibt es noch einen weiteren Vorzug graphischer Analysen: Funktions- und Stufensymbole sind sehr abstrakt und es ist selbst geübten Musikerinnen und Musikern nur sehr schwer möglich, sich unter diesen Symbolen etwas konkret Klingendes vorzustellen. Diagramme der graphischen Analyse hingegen bestehen aus Noten und lassen sich sehr gut hören, am Klavier spielen und mit der analysierten Musik in Verbindung bringen. Der Wert einer graphischen Analyse liegt dabei letztendlich in der Stimmigkeit, die zwischen dem Analysediagramm und der analysierten Komposition besteht. Analysediagramme bieten somit eine Möglichkeit, ohne Sprache und nur mithilfe von Notenschrift zu veranschaulichen, wie wir eine bestimmte Musik wahrnehmen, was sich am besten anhand eines bekannten Musikbeispiels veranschaulichen lässt.
Die Sonate ›facile‹ KV 545 von W. A. Mozart als Beispiel
Das erste Notenbeispiel zeigt den Beginn der Sonate ›facile‹ von W. A. Mozart in der Formfunktion Hauptsatz:
W. A. Mozart, Sonate für Klavier in C-Dur KV 545, Anfang
Klavier: Walter Gieseking, Seraphim Records ID-6049 (1955), Urheberrecht: Public Domain.
Der Hauptsatz, in Schichten zerlegt...
Wenn man eine graphische Analyse erstellen möchte, ist es ein guter Anfang, Melodien in der rechten Hand ohne Verzierungen und Dreiklangsbrechungen in der linken als Akkordsatz zu notieren. Das folgende Notenbeispiel zeigt die Takte 1–4 der Sonate ›facile‹ in dieser Form:
Der Weg zu einer graphischen Analyse besteht anschließend in einer weiteren Reduktion, z.B. indem man Stimmverdoppelungen sowie alle Töne löscht, die nicht zur Darstellung der kontrapunktischen Struktur des Satzes benötigt werden. Notenwerte und Hälse haben dabei keine rhythmische Funktion, sondern geben das Gewicht einer Note an: Eine halbe Note ist gewichtiger als eine viertel, eine viertel gewichtiger als eine achtel, eine Note mit Hals gewichtiger als eine Note ohne Hals usw.
Ein Charakteristikum graphischer Analysediagramme sind Bögen. Sie zeigen keine Artikulation (Legato) an, sondern die Zusammengehörigkeit von Tönen, was der Veranschaulichung musikalische Phrasen dient:
- Der oberste Bindebogen markiert die ersten vier Takte als eine zusammengehörige Taktgruppe.
- Der erste Bogen auf der zweiten Ebene von oben veranschaulicht die Zusammengehörigkeit der ersten drei Töne c-e-g in der Melodie. Da der Bogen die Töne h-c nicht mit umfasst, deutet er darauf hin, dass diese Töne zu einer anderen Stimme (eines imaginären mehrstimmigen Satzes) gehören.
- Der zweite Bogen auf dieser Ebene zeigt an, dass man das g des zweiten und das a des dritten Taktes in der Melodie aufgrund der Lage im Klangraum als zusammengehörig empfinden kann.
- Und der letzte Bogen auf dieser Ebene gibt Auskunft darüber, dass man den Ton g zum Beginn des vierten Taktes auch als Vorhalt wahrnehmen kann.
- Die Bögen ganz unten gliedern die Phrasen der Unterstimme in c-d-c (Tenorklausel in den Takten 1−2) und c-h-c (Sopranklausel in den Takten 3−4).
- Die übrigen Bögen gehören zur Mittelstimme und gliedern diese in c-h-c (Sopranklausel in den Takten 1−2) sowie das Tetrachord f-e-d-c (in den Takten 3−4).
Eine Besonderheit graphischer Analysen zeigt sich in den Balken. Auch die Funktion der Balken unterscheidet sich von ihrem herkömmlichen Gebrauch, weil große Notenwerte verbunden werden und diese sogar weit auseinander liegen können. In dieser Verwendung sind die Balken nur auf einer sehr abstrakten Ebene und damit vielleicht am schwierigsten zu verstehen:
- Der auffällige Balken zwischen einer nach oben und einer nach unten gehalsten Note verbindet in diesem Beispiel das erste c und das letzte e der Melodie. Um diese Zusammengehörigkeit zu verstehen, muss man den Stufenbegriff von Heinrich Schenker kennen: Nach Schenker ist eine Stufe »eine höhere abstrakte Einheit«, die »zuweilen mehrere Harmonien konsumiert, von denen jede einzelne sich als selbständiger Dreiklang oder Vierklang betrachten ließe« (Schenker, Harmonielehre, S. 181). In diesem Sinne lassen sich die ersten vier Takten als Auskomponierung der I. Stufe (C-Dur) interpretieren, wozu Mozart die Harmonien G-Dur und F-Dur verwendet hat. Aus historischer Perspektive würde man wahrscheinlich sagen, dass die Gestaltung des Hauptsatzes mithilfe von Generalbassmodellen bzw. der Harmoniefolgen I-V-I und IV-I-V-I erfolgt ist. Im Schenker-Fachjargon sind die Takte 1−4 eine Prolongation der I. Stufe. Und der Balken zeigt an den Rändern der Prolongation oder Auskomponierung (c im ersten Takt und e im vierten Takt) einen Lagenwechsel an, was Schenker als Brechung des Intervalls c-e bezeichnet. Brechungen funktionieren dabei im Prinzip so wie ein Akkord-Arpeggio (in eine Richtung), nur dass eben auch Intervalle gebrochen werden können und der zeitliche Abstand zwischen den Tönen einer Brechung recht groß sein kann.
- Schenkers Balken sind oft auf einer abstrakten − und deshalb gerne verspotteten − Ebene (dem oben erwähnten Hintergrund) angesiedelt, wobei der Theoretiker auf dieser Ebene nur Sekundschritte abwärts zulässt. Die arabische Zahl mit einem Hütchen über dem Ton e gibt in dem Diagramm darüber Auskunft, dass dieser Ton als ein Ereignis im Hintergrund interpretiert wird (im Gegensatz zu Mozarts motivischer Ausarbeitung im Vordergrund). Dass der zu der Brechung gehörige Ton e wichtig ist, lässt sich zudem an der Notation (Halbe, Hals, Balken) ablesen, wobei eine Besonderheit der kleine nach rechts weisende Balken ist: Er zeigt an, dass in Mozarts Komposition irgendwann der strukturell wichtige Ton d erklingen wird (Sie erinnern sich: im Hintergrund lässt Schenker nur eine Bewegung schrittweise abwärts zu) und an diesem d wird dann ein nach links weisender Balken ersichtlich machen, dass ihm der Ton e vorausgegangen ist. Neben der Brechung werden auch solche Tonleiterbewegungen abwärts im Hintergrund (strukturelle Stufengänge) durch einen Balken gekennzeichnet.
Nach Heinrich Schenker gehören strukturelle Stufengänge im Hintergrund (8−1, 5−1 oder 3−1) zur Musik wie ein Skelett zum Menschen. Den Begriff der Urlinie verwendet er hierfür erstmalig 1920 in seinen Schriften. In der Folge hat Schenker die Urlinie zu einem umfassenden Konzept ausgearbeitet:

H. Schenker, Der freie Satz, Wien 1935,
Anfang (Figurentafeln), Figuren 9−11, S. 2.
Die Figuren 9−11 aus dem Anhang (Figurentafeln) seines Hauptwerks Der freie Satz zeigen die drei möglichen Hintergrundbewegungen, die in einer Konsonanz des Tonikadreiklangs beginnen müssen, also in der Oktave, Quinte oder Terz. Zum Konzept der Urlinie gehört außerdem die Bassbrechung bzw. die Bassbewegung I-V, die an verschiedenen Punkten des Verlaufs eintreten kann, jedoch immer mit der Bassbewegung V-I zu dem Sekunsschritt 2-1 eine Komposition beenden muss. Da dreiteilige Formen wie z.B. Sonaten eine Reprise haben (die in der Regel wie der Anfang beginnt), hat Schenker die sogenannte Unterbrechungsform eingeführt.
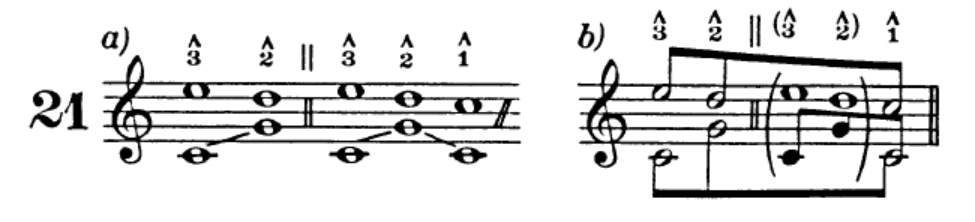
H. Schenker, Der freie Satz, Wien 1935,
Anfang (Figurentafeln), Figur 21, S. 8.
In diesem Modell korrespondiert die Bewegung 3-2 in der Urlinie mit der Modulation in die Oberquinte (I-V), die Durchführung bzw. der Mittelteil unterbricht die Bewegung der Urlinie, die in der Reprise durch einen Rücksprung auf das Niveau des Anfangs wieder aufgegriffen wird und zum strukturellen Schluss der Komposition führt. Mit diesem Modell lässt sich tatsächlich manchmal erklären, warum man in einer Komposition einen Schluss hören kann, obwohl das Stück noch nicht zu Ende ist (denn erreicht wird nur der strukturelle Schluss im Hintergrund, im Vordergrund kann es durchaus noch eine Weile weitergehen). Das in der Figur 21 b) gezeigte Modell verwendet Schenker auch zur Analyse der Sonate ›facile‹, mit dem analysierten Hauptsatz haben wir den ersten Ton des Ursatzes erreicht. Doch wenden wir uns noch einmal dem Vordergrund zu und analysieren mithilfe der graphischen Analyse die nächste Taktgruppe aus dem Kopfsatz der Sonate KV 545.
Die Schichten der Überleitung
Die Überleitung hat Mozart mithilfe eines sehr gebräuchlichen Harmoniemodells gestaltet (IV-I-V-I + Kadenz):
In dem folgenden Beispiel wurden in dem unteren Systemen die Sechzehntelläufe sowie der Rhythmus der Begleitung in den Takten 5−9 weggelassen. Die ›rauschende‹ Bewegung ist dabei für den Charakter einer Überleitung sehr charakteristisch. Dadurch ergibt sich das folgende Diagramm:
Das nächste Beispiel zeigt die letzte Reduktionsstufe noch ohne Bögen und Balken. In diesem Schritt können gegebenenfalls auch die Stimmlagen verändert werden, damit sich ein möglichst gut klingender Satz in nur einem System herstellen lässt:
Wobei die Bögen und Balken dann die Zusammengehörigkeit von Tönen kennzeichnen. Achten Sie darauf, dass hier das oben erwähnte d erklingt, das mit einem Balken nach links versehen worden ist, damit die Beziehung der Töne e am Ende des 4. Taktes und d im 9. Takt erkenntlich wird. An dieser formal wichtige Stelle erklingt die Subdominante als Signal der Kadenz bzw. des Halbschlusses, der den Seitensatz ankündigt. Die Subdominante sieht Schenker wiederum nur als Prolongation der Dominante an, ein zweiter Ton in der Oberstimme in Verbindung mit dem Dominantgrundton im Bass bilden einen wichtigen Halbschluss (in diesem Fall den Quintabsatz der Ausgangstonart nach Heinrich Christoph Koch).
Die Schichten des Seitensatzes
Der Seitensatz besteht aus einer Taktgruppe und ihrer Wiederholung. Er entspricht in seiner Länge dem Hauptsatz (4 Takte) und hat mit 14% − gemessen an der Länge der Exposition − eine charakteristische Länge bzw. Ausdehnung:
Der Seitensatz lässt sich recht einfach auf einen aus Tonika und Dominante bestehenden Akkordsatz reduzieren:
In der nächsten Reduktion wurden einige Akkordtöne weggelassen, jedoch zwei lineare Gestaltungen bei den Taktübergängen aufgenommen. In der Melodie sind diese Linien an den Taktübergängen vom ersten zum zweiten und vom dritten zum vierten Takt zu hören, in der Unterstimmer erklingen sie in der Sechzehntelbewegung des zweiten und vierten Taktes:
Abschließend wird die Zusammengehörigkeit von Tönen wieder mit Bögen und Balken gekennzeichnet:
Die Schichten der Schlussgruppe
Eine Eigenschaft der Formfunktion Schlussgruppe besteht im nachdrücklichen Erreichen der Nebentonart. Nicht selten geschieht dies über eine groß angelegte Kadenz, die Wolfgang Gersthofer in Anlehnung an die Bravour-Arien des ausgehenden 18. Jahrhunderts als Arientriller-Kadenz bezeichnet hat. Oftmals wird die Kadenz durch einen Sextakkord, ein harmonisches Pendeln (z.B. T-D-T) oder eine Sequenz eingeleitet:
Das folgende Diagramm zeigt eine Reduktion der Sechzehntelbewegung auf einen Gerüstsatz in großen Notenwerten:
Dieser Satz wird auf die bekannte Art noch einmal reduziert und in ein Notensystem gebracht:
Wobei der letzte Schritt wieder der Kenntlichmachung von Zusammengehörigkeiten durch Bögen und Balken besteht:
Und dieses strukturelle Erreichen des Grundtons verbunden mit einer Kadenz hören wir als den eigentlichen Schluss der Exposition, auch wenn anschließend wie im Falle der Facile Sonate noch einige Takte (und im Falle Beethovens noch einige Minuten) komponierter Musik folgen können.
Schenkers Analysen
Nach den bisherigen Ausführungen dürften der lesende und hörende Nachvollzug der originalen Analysen von Heinrich Schenker keine Probleme mehr bereiten. Das erste Diagramm ist Teil einer Analyse des ganzen Kopfsatzes, die Schenker im 4. Heft der Zeitschrift Der Tonwille im Jahr 1923 publiziert hat:

H. Schenker, Der Tonwille (1923),
Heft 4, Beilage
Die drei folgenden Diagramme finden sich in den Figurentafeln zu der späten Publikation Der freie Satz. Das erste Beispiel, die Figur 47, Nr. 1, zeigt eine Analyse des ganzen Kopfsatzes (der Text dazu findet sich im § 150). Die Abstraktheit von Diagramme dieser Art führt bei Musikerinnen und Musikern, denen die Zwischenschritte zu einer graphischen Analyse nicht bekannt sind, oftmals zu Unverständnis und Ablehnung:

H. Schenker, Der freie Satz, Wien 1935,
Anfang (Figurentafeln), Figur 88, c), S. 44.
Die Brechung am Anfang (das war die spezielle Balkung der Töne c-e) erlaubt eine schnelle Orientierung zwischen diesem Diagramm und einer Analyse des Hauptsatzes und der Überleitung, die Schenker in der Figur 124 skizziert und in den §§ 260 und 330 erläutert hat:

H. Schenker, Der freie Satz, Wien 1935,
Anfang (Figurentafeln), Figur 124, Nr. 5a) S. 82.
In dem abstrakten Diagramm für die ganze Sonate ist auch die Sequenz zum Beginn der Schlussgruppe nicht zu sehen. Die Abwärtsbewegung vom d''' zum g'' vor dem Doppelstrich konkretisiert Schenker in der Figur 88c, die im § 213 erläutert wird:

H. Schenker, Der freie Satz, Wien 1935,
Anfang (Figurentafeln), Figur 21, S. 8.
Formfunktionen und strukturelle Einheit
Schenkers Analysen weisen sowohl die hier als Hauptsatz und Überleitung als auch die als Seitensatz und Schlussgruppe bezeichneten Taktgruppen als (strukturelle) Einheiten aus. Der Seitensatz wird dabei als Auskomponierung des Tons d verstanden und in der Schlussgruppe führt der Quintzug d-g in den Grundton der Nebentonart. Die Analysen englischsprachiger Autoren wie William E. Caplins und Hepokoski/Darcy korrespondieren mit diesen Analysen, z.B. bilden nach Caplin der Seitensatz und die Schlussgruppe einen (expanded) sentence, den er als subordinate theme bzw. Seitensatz interpretiert. Allein aufgrund solcher Übereinstimmungen scheinen Caplins Formfunktionen in einem größeren Maße der in Nordamerika mächtigen Schenker-Tradition verpflichtet zu sein, als es der Autor glauben mag. Aufgrund einer fehlenden Kadenz am Ende des vierten Taktes bezeichnen Hepokoski/Darcy auch den ersten Teil dieser Exposition als sentence (»Therefor they do not constitute a phrase − only a modul (or a complementary pair of two-bar modules. The sentence continuation module begins in mm. 5−8 [...]«), was es sogar ermöglicht, die Takte 1−12 der Facile-Sonate als öffnenden Vordersatz und die Takte 14−26 als schließenden Nachsatz einer Periode zu bezeichnen. Die Verwendung der Modelle Satz und Periode auf einer höheren Ebene bzw. quasi im Hintergrund ist dabei für nordamerikanische Musiktheorie charakteristisch und dürfte − wie bereits erwähnt − durch die Analysen nach Heinrich Schenker beeinflusst worden sein. Die Folge, dass auf der höchsten Ebene damit nicht mehr die extrinsisch bestimmbaren Formfunktionen, sondern nur noch intrinsisch bestimmbare Strukturmodelle zur Verfügung stehen, kann sich gelegentlich als Vorzug, in vielen Fällen jedoch als Nachteil erweisen. In dem folgenden Video wird diese Auffassung als dogmatisch kritisiert und die hier vorgeschlagene Begriffsverwendung erläutert.
Angemessenheit und didaktische Dimension
Eingangs wurde erwähnt, dass der Wert bzw. die Qualität einer graphischen Analyse letztendlich von der Stimmigkeit zwischen dem Analysediagramm und der analysierten Komposition abhängt. In den Diagrammen zu den einzelnen Formfunktionen wurde zwar schon auf die Stimmigkeit geachtet, doch eine abschließende Beurteilung sollte mindestens die ganze Exposition (im Idealfall sogar den ganzen Satz) im Blick behalten. Hören Sie sich die verschiedenen Ebenen des Diagramms gleichzeitig zur Musik der Sonate ›facile‹ an und entscheiden Sie über das Hören, ob sie ein Detail als störend empfinden, das wir mithilfe der graphische Analyse aus dem originalen Notentext entwickelt haben:
Es dürfte dabei auf der Hand liegen, dass die Sinnfälligkeit graphischer Analysen insbesondere aus didaktischer Perspektive ein Vorzug gegenüber anderen musiktheoretischen Chiffrierungssystemen darstellt, denn es braucht nicht viel Fantasie sich vorzustellen, dass Sätze, die sich an einer Analyse nach Heinrich Schenker orientieren, aufgrund ihrer Einfachheit als Mitspielsätze im Klassenzimmer besonders geeignet sind und dass sich durch eine solche musikalischen Praxis sogar das strukturelle Hören tonaler Musik fördern lässt:
Die Auswahl der Töne, die wir für die graphische Analyse ausgewählt haben, ist so, jedoch auch anders möglich. Oder in der Fachsprache der konstruktivistischen Systemtheorie: die Selektion ist kontingent. Es wäre daher irrig zu glauben, Ziel einer graphischen Analyse sei es, eine einzig richtige Interpretation oder Hörweise für eine bestimmte Komposition zu finden. Jede Komposition erlaubt verschiedene Hörperspektiven und beim Vergleichen von Analysen prominenter nordamerikanischer Autoren wird schnell ersichtlich, dass es auch auf professioneller Ebene divergierende Analysen zu einem bestimmten Stück gibt. Beim Erstellen eines Diagramm ist man allerdings gewzungen, sich über die Funktion vieler Details Gedanken zu machen, was dabei hilft, ein Stück immer besser kennenzulernen und durchhören zu können. Schenker hat dazu angemerkt:
In der Musik ist es eben wichtig, sehr wichtig, jede Erscheinung, selbst die kleinste, zu beachten und jedes einzelne Detail, selbst das Geringste, mit der ihm eigenen Ursachen zu hören. Weil man so hörend nicht nur dem Künstlern am besten gerecht wird, sondern der Musik überhaupt.
Heinrich Schenker, Harmonielehre, 1906, S. 103.
Und er warnt davor:
O, wie leicht ist Theorie und Musikgeschichte fabriziert, wenn man schlecht hört!
Heinrich Schenker, Harmonielehre, 1906, S. 102.
Natürlich war Schenker davon überzeugt, dass sein Hören das einzig wahre ist, was uns zu einigen Widerständen führt, die der Beschäftigung mit Schenkers Theorie in Deutschland entgegenstehen.
Widerstände und Perspektiven
Dafür, dass die Lehre Heinrich Schenkers in Deutschland nur zögerlich aufgenommen worden ist (und außer in kleinen Forschungskreisen heute immer noch weitgehend ignoriert wird), lässt sich nicht nur die Naziherrschaft verantwortlich machen. Die Schuld liegt auch bei Heinrich Schenker selbst. Seine kleinkarierten Polemiken (»Man weiß ja, wie es die Kinder mit den Puppen treiben [...] Nicht anders machen es nun auch die Theoretiker mit ihren Tonpuppen«), seine zuweilen gehässige Sprache (z.B. »Ohrfinsterling« zu H. Riemann), seine nationale Hybris (»Wie kann sich nun aber das deutsche Volk aus dieser Not erretten und auch der übrigen Menschheit den Weg zum Heile weisen?«), seine persönliche Überheblichkeit (»Der Durchschnittsmensch ist ein Wiederkäuer seiner Einbildung [...]«), seine ablehnende Haltungen gegenüber der Neuen Musik (»Dort ein S. Bach, Haydn, Mozart, Beethoven, Schubert, Schumann, Mendelssohn, Brahms − welche Fülle! Hier ein Strauß, Pfitzner, Humperding, Mahler, Reger − welche Armut!«) und nicht zuletzt auch seine befremdlichen politische Ansichten (»Es ist während des Weltkriegs schnöder Verrat geübt worden am Genie des Deutschtums und am Genie der für alle Zeiten denkwürdigen Heerführer Hindenburg und Ludendorff [...]«) sind ein wirklich hartes Brett, wenn man sich anhand der Originalschriften durch Schenkers Musiktheorie bohren bzw. ernsthaft mit der graphischen Analyse auseinandersetzen möchte. Die Entwicklungen in Amerika hingegen haben gut durchdachte Lehrbücher ermöglicht, die einem die verbalen Ausfälle Schenkers ersparen und die Konzentration auf seine musikbezogenen Aussagen erleichtern.
Dessen ungeachtet hat Heinrich Schenker eine echte Musiktheorie hinterlassen. Eine Theorie, die Aussagen über Musik trifft (z.B. dass Züge im Hintergrund immer in der Oktave, Quinte oder Terz eines Tonika-Klangs beginnen müssen, dass es im Hintergrund nur Stufenbewegungen abwärts geben kann usw.), die deswegen ›falsifizierbar‹ ist bzw. sich in Bezug auf eine bestimmte Musik auch als unangemessen erweisen kann (die sogenannte Stufentheorie ist in diesem Sinne z.B. keine Theorie, sondern lediglich eine Methode, da sich mit ihr keine Aussagen verbinden, welche Harmonien aufeinander folgen dürfen). Eine pragmatische Möglichkeit im Umgang Schenker besteht darin, seine Theorie nur partiell oder gar nicht nicht zu teilen und dennoch seine graphische Analyse als Methode zu verwenden, zumal für die Zusammengehörigkeit von Tönen auch andere Erklärungsmodi denkbar sind (z.B. über das Gesetz der guten Gestalt bzw. der Einfachheit oder Prägnanz der Gestaltpsychologie). Felix Salzer z.B. hat auf einige Theoreme aus Schenkers Theorie verzichtet, um die graphische Analyse für das Hören freitonaler Werke des 20. Jahrhundert nutzbar machen zu können. In diesem Sinne veranschaulichen Diagramme der graphischen Analyse eine willkürliche (nicht jedoch beliebige) Auswahl an Tönen, die man für eine spezifische musikalische Wirkung einer Komposition als bedeutsam interpretiert. Nicht mehr, aber auch nicht weniger...
Literatur
- William E. Caplin, Classical Form. A Theory of Formal Functions for the Instrumental Music of Haydn, Mozart, and Beethoven, New York 1998.
- Ulrich Kaiser, »Formfunktionen der Sonatenform. Ein Beitrag zur Sonatentheorie auf der Grundlage einer Kritik an William E. Caplins Verständnis von Formfunktionen«, in: ZGMTH 15/1, 29–79. https://doi.org/10.31751/956
- Erwin Ratz, Einführung in die musikalische Formenlehre. Über Formprinzipien in den Inventionen J.S. Bachs und ihre Bedeutung für die Kompositionstechnik Beethovens, Wien 1951.
- Schenker Heinrich, Der Tonwille. Flugblätter zum Zeugnis unwandelbarer Gesetze der Tonkunst einer neuen Jugend dargebracht, 10 Bde. Wien und Leipzig 1921–1924, Ausgabe in 3 Bdn. Wien 1924.
- Heinrich Schenker, Neue musikalische Theorien und Phantasien. Bd. II: Kontrapunkt, 2 Bde., Berlin 1910.
- Heinrich Schenker, Neue musikalische Theorien und Phantasien. Bd. III: Der freie Satz, Wien 1935, 2/1956.
Erstellung des Beitrags: 2. Mai 2021
Letzte Änderung des Beitrags am 7. Mai 2021
Erstellung des Beitrags: 2. Mai 2021
Letzte Änderung des Beitrags am 7. Mai 2021